Quanta, Quantization, and the Myth of Quantised Gravity.

In 1905, Einstein famously published four papers, each of which caused a revolution in physics. Although he is better known for his theory of relativity, it was his 1905 explanation of the photoelectric effect that won him a Nobel Prize.

In the photoelectric effect, UV radiation falling on the surface of a metal can make the metal emit electrons. This turned out to be difficult to explain based on the then-current theory of light as a wave. Experimenters had observed that the kinetic energy of the emitted electrons depends on the frequency of the radiation, not the intensity. The wave theory of light predicts that intensity will be the controlling variable. Moreover, the effect has a threshold frequency, below which no effect is seen.

Max Planck had already postulated that light also had a particle nature. Einstein applied this idea to explain the photoelectric effect, arguing that light consisted of packets of energy and that an electron absorbed all of it or none of it. We now call such a packet a quantum (Latin for "How much?".) We call a quantum of electromagnetic radiation a photon.

In the first essay in this series, I suggested that, given the role of atoms in energy quantisation, we should see quantisation as a structural (aka "emergent") property, rather than a substantive (aka fundamental) property. In this essay, I will pursue this argument a little further and then comment on the myth of quantised gravity.

What is and is not Quantised?

Quantisation is simply a fact of nature. Some quantities are naturally quantised. These include

• Franck-Hertz experiment (1914): Showed electrons in gases absorb energy in discrete steps.
• Stern-Gerlach (1922): Silver atoms deflect in discrete trajectories, proving spin quantization.
• Zeeman effect (1896): Magnetic fields split spectral lines into discrete frequencies.
• Neutron interferometry (1970s): Confirms half-integer spin for fermions.
• Millikan’s oil drop (1911): Measured charge strictly as ne.
• Quantum Hall effect (1980): Conductance steps at e²/h

However, we know of several quantities for which there is no evidence of quantisation.

• Space and Time: No experiment has ever detected quantized spacetime.
• Mass: There is no evidence of a discrete unit of mass. And again, no observation requires it.
• Gravitational waves show no signs of discreteness. No quantum theory of gravity successfully describes observation. And no explanation of an observation so far made requires quantum gravity.
• Fluids/Collective Phenomena: Sound waves, ocean waves, etc., are not discrete.

At present, it is still unfortunately the case that quantum theory has not offered us any coherent explanation of the atom or subatomic world. There is certainly no reason to believe that quantum physics explains anything at all about the world in its current state. It's merely a mathematical formalism that accurately predicts the probabilities of all outcomes for any observation.

Attempts to find the physical meaning of this have amounted to reifying the probability distribution. I will cover the metaphysics of probability in my next essay.

For now, we can simply note that no attempt to reify the wavefunction has resulted in a coherent metaphysics. We are left with a number of mutually exclusive metaphysical speculations that manage to "explain" quantum mechanics at the cost of having to abandon Realism and locality.

99% of physicists are apparently willing to pay this toll. While a dogged band of eccentric tenured professors (who can't be sacked for heresy) and a ragged collection of outsiders continue to try to do better and rescue Realism in the process. This essay, and the previous two, are my reflections on how we could do better.

Particles and Properties

In my view, the term "particle" is confusing. For physicists, it continues to conjure the idea of a point mass, which is to say a particle that has mass but no length dimensions. The problem with point masses is that density is mass divided by length. If an electron had finite mass but zero length (radius or volume), it would have infinite density since x/0 = ∞; for all values of x. That is to say, every electron would be a tiny blackhole. Observation tells us this is not the case. So we can simply, logically, rule out any talk of "point masses" or "point charges". They are mathematical fictions. 

We often assume, for the purposes of calculation that all the mass of an object is concentrated at the centre of mass. This massively simplifies mechanics. But it is precisely in atomic physics that such idealised models run into trouble.

In our universe, there are no points, no singularities, and no infinities (though some quantities may be uncountable). The same observation means that general relativity is incomplete, since it currently predicts singularities in black holes and at the Big Bang. Indeed, at the Big Bang, all energy was supposedly contained within a tiny volume, creating near-infinite spacetime curvature. If the universe started out that way, then it was a black hole, and nothing ever escapes from a black hole. There are dozens of ideas about how to prevent singularities in GR, but as far as I can see, there is no consensus on the horizon.

Wave-particle duality made enough sense in the 1920s that no one seriously questioned it. In the 2020s, however, it has become clear that "particle-like" behaviour is an artefact of detector design and, as I have explain, related to the standing wave structure of the atom. Matter is waves (likely soliton waves in spacetime). However, this realisation did not lead professional physicists to go back to the original formulations and root out all mention of particles. Rather, wave-particle duality is still retained as a fundamental postulate even in quantum field theory. 

To put it another way, one of the quantities that physicists still use the maths for is to find the "position" of the electron in an atom. And one way of talking about superposition is that the electron in an atom is in all possible locations at once (hence the idea of electron "clouds". But note that the mass of all these superpositions is still just the mass of the electron. I'm not sure how this can be explained. Can an electron in a superposition have fractional mass? When you ask physicists this is the kind of question that they seem to struggle. I assume that this is because the question is not canonical. The answer is not in the textbooks. 

That said, the electron-as-wave has a very clear physical reality. The electron has mass, charge, and angular momentum. These are all real quantities that can be measured. Moreover, electron interact in causal ways. So the electron behaves like a real object with objective properties that can be measured precisely. So why the formalism is so vague I do not understand. But since "particle" is inaccurate and carries baggage, I propose to use the term wavicle for such objects.

I discussed the roles of substance and structure in reality at length in a series of three essays in 2016. In the meantime, I've decided to drop the terms "fundamental" and "emergent", which are legacies of metaphysical reductionism. Reductionism holds that only the irreducible (i.e. "fundamental") features of the world are real. In this view, "real" and "fundamental" are synonyms. The corollary is that structure is not real. I reject this notion.

I take structure to be every bit as real as substance. For example, structure can persist over time, we can interact with structures as objects (over and above any interaction with their parts), and structure is capable of participating in sequences of events that appear causal. 

Note, I need to go back over the issue of causality. Since the last time I wrote about it, I've learned that causality is, in fact, built into relativity. Relativity takes as axiomatic the idea that causality is independent of frame of reference. Time and space are relative to one's frame of reference, but causality is not.

While reductionism is the optimal approach for studying substances, it gives us no leverage on understanding structures. Most of the significant properties of water, for example, are due to the arrangement of the three atoms that make up the molecule. For example, while both hydrogen and oxygen atoms are electrically neutral, the water molecule is an electric dipole. As such, electrostatic forces created by the dipole play a significant role in how water behaves. This is why, for example, water has such a high surface tension and a high specific heat compared to similar liquids.

In my view (influenced by Jones 2013), there are two kinds of properties.

1. Substantial Properties are the result of substance. Substantial properties are unaffected by the imposition of structure (no "downward" causation).
2. Structural Properties are the result of structure. Structural properties are (at least to some extent) independent of substance.

This is a static view. If we need to talk about a dynamic structure, it can be helpful to switch to the language of systems and speak of systemic properties. A "system" is simply a persistent dynamic structure. And a structure is a static system. Keep in mind that "static" and "dynamic" are idealisations. In the real world, things are always in motion, even those that persist over time.

How we perceive such systems is affected by the scale on which we observe them. On the millimetre scale, for example, few objects are as stable and unchanging as diamonds, which were formed in the mantle of the Earth millions of years ago. On the picometer scale, the diamond resolves into a vibrating lattice of vibrating atoms, with everything in constant motion. Matter is vibrant.

Whether we experience it as a static structure (a diamond) or a dynamic system (vibrating lattice) depends on scale. There's inevitably a transition zone in which making the distinction is difficult. We simply choose whichever viewpoint suits our aims.

That said, I think the substance/structure gestalt is helpful for anyone wishing to move beyond the limits of reductionism and into a more coherent view of reality. After all, almost everything that we can interact with is a structure or system. And our language about the world is based on how we physically interact with such objects.

Quantisation of Energy

In my first attempt at a description of the hydrogen atom, I described the electron as a (real) spherical standing wave (I leave open for the time being the question of what is waving, but I'm leaning towards the answer being "spacetime"). The basic idea is not new; both Heisenberg and Schrodinger started off with a similar approach. The difference is that they start off assuming wave-particle duality, which we now know to be a false step. Let's look again at the concept of a standing wave.

Standing Waves on a String

A guitar string is anchored at the ends by the "bridge" and the "nut". No matter how much a string is vibrating, the amplitude of vibration at the ends is always zero. We call these points nodes. If I tune a guitar string to a pitch and strike it, other things being equal, it will always vibrate at that precise pitch (pitch is determined by the density of the material, the radius of the string, temperature, and the tension it is under). 

Note that because the ends of the string are anchored and cannot vibrate, a guitar string is only capable of vibrating in standing waves. Once you impose boundary conditions such as anchoring the ends, the oscillations can only be standing waves.

Standing waves form on a guitar string when we strike it. Striking the string causes it to be locally stretched out of shape and experience a restoring force so that the stretched part accelerates back towards the centre but overshoots. The restoring force always acts towards where the resting state would be. This perturbation travels along the string in both directions. When it reaches the bridge or nut, the perturbation is reflected back along the string in the opposite direction.

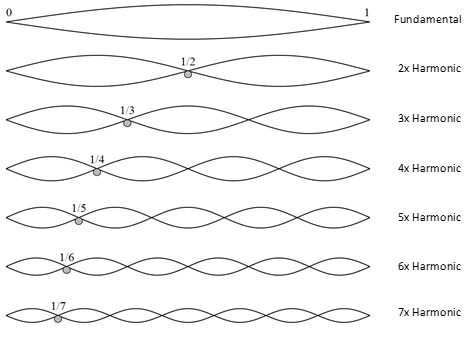
If you think about how wavelength is defined in terms of sine waves (crest to crest), you can see that nodes correspond to where a cycle of the sine wave crosses the x-axis, i.e. at 0, π, and 2π radians. Thus, other things being equal, the fundamental mode (= "ground state" for an electron) corresponds to a wavelength of twice the string length.

Other things being equal, the string can also vibrate at higher energies, with pitches corresponding to the string length (L) divided by a positive integer.

For example, I can make a guitar string vibrate in the first harmonic mode. This is done by lightly placing a finger on the string at the halfway point (the 12th fret) to prevent it vibrating there, and striking the string with the other hand. This forces the string to vibrate at twice the frequency, with zero amplitude at the ends and in the middle. Now there is a node (zero amplitude) in the middle of the string as well as at the ends, corresponding to a whole wavelength. If the wavelength is halved, the frequency doubles. In music, we call this first harmonic the octave (referencing the fact that there are seven unevenly spaced notes in diatonic scales).

One can make the string vibrate at L/3 by damping the oscillations at 1/3 of the string length. In the case of a guitar, this corresponds to having nodes over the 7th and 19th frets. The second harmonic has a frequency of 3/2 of the fundamental. In music terms, this is an octave and a fifth above the fundamental.

Note that for n > 3, the nodes are no longer precisely aligned to the frets because the spacing between them is based on an equal temperament scale, to allow the guitar to sound in tune across different keys. 

Also, in real life, guitar strings vibrate in two dimensions, and/or the plane of vibration may precess around the axis of the string. Strings also vibrate in many modes at once, and, in practice, the first harmonic is often more prominent than the fundamental.

There are many videos online explaining this, so if my explanation is not clear to you, I recommend looking up "harmonics". This video gives you a decent brief intro plus some basic maths.

Note. Some people refer to the fundamental as the "first harmonic". As a musician, I think of harmonics as additional modes of vibration. So the "first harmonic" in my view is the octave.

Standing Waves in a Sphere

As noted, in order to balance the spherically symmetric electric field of the proton, the electron in a H atom must be configured as a sphere. Any other configuration leaves the electrostatic field unbalanced, meaning that the atom would not be electrically neutral. However, all atoms are electrically neutral.

Ergo, electrons in atoms are spherical with the nucleus at the centre of the sphere. The nuclear reaction of an electron and a proton to form a neutron (and a neutrino) is endothermic, requiring energy to make it happen. This means that it is not thermodynamically favoured despite the strong electromagnetic attraction. And this means that electrons seldom combine with protons except in places like the core of stars.

Keep in mind here that I'm describing an idealised situation in which no external forces are acting on the atom. In reality, everything influences everything else via the four forces.

Still, the electrostatic attraction between electron and proton is powerful and draws them together, pulling the spherical electron towards the centre. However, the electron wave has to accommodate a minimum number of wavelengths, so, despite the electrostatic attraction, it cannot get any smaller than the size needed to accommodate that number. Attracted inwards, the electron hits the minimum size limit, and it rebounds outwards. Just like the perturbation on a guitar string reflecting off the bridge and nut. The outgoing wave is prevented from escaping by the electrostatic attraction, which provides the restoring force. The outgoing wave stalls and accelerates back towards the centre again. With two waves of the same wavelength travelling in opposite directions, we have the conditions for the formation of a standing wave. 

Energy radiates away from the guitar string in the form of sound waves and heat. And it gradually loses amplitude but stays at the same frequency. But there is no equivalent of this process in an atom, so the oscillation of the electron goes on indefinitely. Each atom is a kind of perpetual motion machine.

A logical consequence of this is that energy absorbed from or emitted by atoms will be quantised. The only way a resting state (fundamental) standing wave can absorb energy is for it to jump to a harmonic mode of vibration. The actual energies can be predicted from first principles using the maths of spherical standing waves developed by Pierre-Simon Laplace, ca 1782 (long before quantum mechanics was envisaged). Similarly, energy can only be emitted when an electron falls from a higher harmonic to a lower harmonic or to the fundamental.

For similar reasons, if the electron itself is emitted from a hydrogen atom, then it has a very specific energy corresponding to the ground state energy (looked at another way, this is the ionisation potential of the atom). An atom cannot capture an electron with less than the ground state energy. If it captures an electron with more than the ground state, then the excess will be emitted as a photon of that energy.

Outside of the atom, the energy of electrons is not quantised. A free electron can have any energy. Similarly, free photons can have any energy. We can design systems so that they emit photons of any arbitrary wavelength as long as the associated energy is greater than the ground state energy (ca. -13 eV). Any colour of light is possible, and for any two colours, we can always find an intermediate wavelength (even if the human eye can't resolve the difference).

However, note that when we need "free" electrons to study, we have to get them from atoms. So all the electrons we get to study always come pre-quantised. This may have blinded physicists to the role of the standing wave in energy quantisation and caused them to see quantisation as an independent idea.

This account explains the photoelectric effect and the ionisation energy of an atom as natural consequences of the standing wave configuration of the atom. And without invoking quantum mechanics.

Quantisation of "Spin"

A more complete treatment of the angular momenta of wavicles using a theory proposed by Jackson & Minkowski (2021) and similar to Macken's (2024) is in the pipeline. Today, I will just outline the basic idea. Spin is quantised for quite different reasons than energy. In this view, we think of the spherical electron as rotating. As I have shown, simple logic dictates that, in a hydrogen atom, an electron can only be a sphere. Any other configuration leads to unbalanced electrostatic forces and unstable atoms, because the electric field of the proton is spherically symmetrical.

It's less clear that a free electron has a shape, but we can account for at least some of its characteristics by modelling it as a tiny, rotating spherical soliton wave. This approach also comes with some non-trivial problems that I will address in a future essay.

We can illustrate the general principle using the planet Earth as an analogy.

Looked at from above the north pole, the Earth is rotating anticlockwise around the y-axis. Moreover, if I hovered above Cambridge at ~52° north, the Earth is still spinning anticlockwise. And so for any position that is not directly above the equator.

If I look at exactly the same planet from above the south pole, I see it rotating clockwise. Similarly, as I move from the pole (90° S) down towards the equator (0° S), I see the rotation as going clockwise all the way.

Now, if I measure the angular momentum of the Earth on the y-axis, from any angle, the vector will point along the y-axis in the positive direction (i.e. north). If it were spinning clockwise on the y-axis, the vector would point in the negative y-axis. And this is precisely analogous to "quantum spin" having just two values: "up" and "down" (with respect to the axis of measurement). If I measure the y-axis angular momentum of a sphere rotating on some (unknown) arbitrary axis, I will still see it as either pointing to +y or -y.

The analogy of rotation has been historically rejected for two main reasons. One of which was the strange behaviour of the angular momentum of spin ½ wavicles. If we impose a 360° rotation on a spin 1 wavicle, it behaves as expected: if we see it as spin up initially, following a 180° rotation we see it as spin down, and a further 180° rotation (360° in total), we see the spin as up again.

Spin ½ wavicles do not behave like this. If we rotate a spin ½ wavicle, such as an electron, it comes back to spin "up" in just 180° (though this state is not quite identical to the starting position). The hypothetical spin 2 wavicle only returns to spin up in 720°.

As a result, physicists generally abandoned the idea that angular momentum is related to rotation. Instead, they invented the idea of "intrinsic angular momentum", which doesn't involve any actual rotation. This is very dubious from a philosophical point of view. It's an ad hoc assumption that is only justified because it works mathematically, but it cannot be tested. And, in the process, it destroys any hope of a realist description of wavicles. Jackson and Minkowski have shown that we have to allow for gyroscopic effects of magnets in magnetic fields.

The gyroscopic effect is traditionally demonstrated in physics classes by an instructor sitting on a rotating chair holding a bicycle wheel. In this video for example, the wheel is pitching (rotating around the x-axis), the instructor attempts to make it roll (rotation around the z-axis), and the result is torque creating a yawing motion (rotation around the y-axis).

Something analogous seems to be happening to a spin ½ wavicles because they are magnetic dipoles (aka magnets). If a spherical magnet is rotating around the y-axis and I try to flip it around the z-axis using a magnetic field, then there is a torque around the x-axis. The result is that for a spin ½ wavicle that is rotating around the y-axis, a 180° rotation in the z-axis is accompanied by a 180° rotation in the x-axis. The direction of the angular momentum goes from up and back to up. 

But it's not exactly the same, because the 180° rotation in the x-axis leaves the wavicle with reversed orientation in the z-axis. Another 180° rotation in z does bring it back to the starting position.

So for a sphere rotating about the y-axis, subjected to a 180° rotation about the z-axis:

• spin 0 wavicles cannot be rotated by magnetic fields.
• spin 1 involves a 180° rotation in z + 0° rotation in x.
• spin 2 involves a 180° rotation in z + 90° rotation in x.
• spin ½ involves a 180° rotation in z + 180° rotation in x.

This reproduces the observed properties of wavicle angular momentum without abandoning realism. And to date, spin 2 is purely hypothetical. Once again, there is a "classical" description of the system that predicts the behaviour we observe. And it is of a piece with the other classical physics that I have invoked in this series of essays. 

The other, more serious problem with modelling the electron as a sphere is that, based on what was known a century ago, it was calculated that the surface speed of a point on such a sphere would be moving faster than the speed of light. There are ways around this, but it needs a lengthy explanation that I will work through in a forthcoming essay.

Conclusions and Gravity

To be clear, I'm not trying to explain (or justify) the postulates of quantum physics. Indeed, I think that postulates such as a wave-particle duality or fundamental quantisation are false. I am an old-fashioned kind of scientist, and I am only trying to explain observations. Philosophically, I remain committed to pragmatic Realism and the substance/structure gestalt (in place of reductionism).

As far as I can see, quantisation of energy (in experiments like the photoelectric effect) is driven by the structure of atoms, i.e. it results from standing waves, all of which are inherently quantised. It is the structure of the atom rather than the substance of the electron that imposes this configuration on matter. And the quantisation of angular momentum is because the spherical wavicle is rotating, with the proviso that spin ½ wavicles have a magnetic moment (they are magnets), so that using a magnet to rotate the angular momentum in one direction causes an orthogonal torque. This means that we can say:

Quantisation of energy is a structural property of atoms, rather than a substantial property of wavicles.

Or, for those who prefer the less precise legacy terminology:  

Quantisation is an emergent property of atoms, rather than a fundamental property of particles.

And none of this is, in any way, "weird". Rather, we fully expect this behaviour from what we know about the (classical) mechanics of standing waves and spinning magnets. 

An important corollary of this is that, where there is no standing wave involved, we should not expect energy to be quantized because there is no reason for it to be quantised. Where a wavicle is not a rotating sphere, we don't expect angular momentum to be quantised either.

A case in point is the gravitational wave. We have been measuring gravitational waves using the LIGO apparatus for a few years now. Gravitational waves are unequivocally real. The waves we detect are mostly from binaries of black holes or neutron stars colliding. It seems clear that such systems are not stable, and that (therefore) they do not form standing waves. Ergo, we would not expect gravity waves to be quantised.

Despite a century of strenuous efforts by a cadre of maths geniuses, there is still no way to meaningfully quantify gravity using the standard methods of quantum physics. The attempts to quantise gravity have not worked. And we should not expect this to ever work.  

The quest for quantised gravity is not driven by any practical consideration or observation. Quantum gravity is not required to explain any existing experimental observations. Rather, the search for quantum gravity is being driven by ideological and aesthetic concerns. 

Worse, physicists appear to believe that GR and QM ought to be reconcilable while at the same time acknowledging that neither theory is yet complete. My thought is that we cannot expect two incomplete theories to be reconcilable anyway. In all likelihood, completing them will solve the apparent problems. 

Atoms, protons, and electrons are real. They persist over time and have measurable properties such as mass, charge, and angular momentum. In sequences of events, these entities play a causal role. In which case, I cannot see the logic in modelling atoms, protons, or electrons in terms of abstract probabilities. I believe this category error explains why the metaphysics that scientists have drawn from the formalism are so divergent and mutually exclusive: they are not anchored in reality. 

The title of my next essay will be: "Ψ-ontologies and the Nature of Probability."

~~Φ~~

Bibliography

Jackson, Peter A. & Minkowski, John S. (2021). "The Measurement Problem, an Ontological Solution." SpringerNature, Foundations of Physics 51 (article 77).

———. (2014). "Quasi-classical Entanglement, Superposition and Bell Inequalities." Unpublished essay. https://www.academia.edu/9216615/

Jones, Richard H. (2013). Analysis & the Fullness of Reality: An Introduction to Reductionism & Emergence. Jackson Square Books.

Macken, John. (2024). "Oscillating Spacetime: The Foundation of the Universe". Journal of Modern Physics 15 (8): 1097-1143. DOI: 10.4236/jmp.2024.158047

Notes on Early Atomic Models

In attempting to explain quantum mechanics, many authors take the approach of providing a linear historical narrative of "heroic failure" (a theme of special importance to the British). Thomson's "plum pudding" model failed and was replaced by Rutherford's "planetary" model of the atom, which in turn failed and was supplanted by Bohr's model. And Bohr's model was more or less upheld by quantum mechanics (which Bohr helped to formulate). I learned a lot of this "history" at school or picked it up as part of physics folklore.

Lately, I've been searching the literature on the development of quantum mechanics and reading selected papers (and cramming to get my reading level to the required heights). It was with considerable interest, then, that I stumbled on a paper by two Norwegian historians of science, Renstrøm & Bomark (2022). The paper has been posted on the science preprint server, ArXiv (i.e. "archive"), but has not subsequently been published as far as I can see.

The authors compare what is found in physics textbooks to what the founders of atomic physics actually said in their publications. And what they found was a systematic misrepresentation of the facts. As Renstrøm & Bomark say in conclusion:

Physics is perhaps the most exact of all sciences and we pride ourselves with extremely well tested and precise laws that allows us to make firm statements about the world we live in. This should be reflected in the way we present our field to the outside world as well.

My notes and comments on their article follow. I note that the folklore in question has spread to every corner of the internet as well.

Before diving in, I want to comment on the word "model". Although both Thomson and Rutherford published their articles in The Philosophical Magazine, here a "model" is not simply a conceptualisation of the problem, as we might expect in a work of philosophy. In this context, "model" means a mathematical model, i.e. a series of equations that can be used to describe the behaviour of the system in question at any arbitrary time. Most of the original papers that I mention below consist of page after page of complex mathematical calculations that are difficult to follow because they are written for experts who already know the topic and its literature. In this context, the speculations about what the model means in physical terms are secondary (though not unimportant). Like many religious texts, physics papers can often only be understood via commentaries.

Thomson's "Plum Pudding" Model.

Joseph John "J. J." Thomson (1856–1940) won the Nobel Prize for physics in 1906 for his work on the conduction of electricity by gases. This work also led to the discovery of electrons ca 1897. Thomson was the first to demonstrate that electrons—Thomson called them corpuscles—can appear to behave like particles. It took some time for the idea to catch on, however.

Up to this point, it was assumed that electrons were waves, like light. During this period, X-rays were discovered, which led to the realisation that light, X-rays and various other forms of radiation (UV, IR, radio, microwave) were all related. Indeed, they are the same phenomenon, at different wavelengths.

Thomson was able to experimentally estimate the mass and mass-to-charge ratio of the electron, accurately noting that the electron was of the order of 0.1% of the mass of the atom. Thomson (1906) showed that the number of electrons in an atom was "of the same order as the atomic weight".

The standard narrative is that Thomson proposed an atomic model in which negatively charged electrons were distributed in a sphere of positive charge, like "plums in a[n English] pudding" or "raisins in a cake". Encyclopedia Britannica, the acme of a reliable source, repeats this spiel and provides a helpful illustration:

Renstrøm & Bomark note that this static picture with randomly distributed electrons is what physics textbooks also give. It is part of physics folklore. And if you search online for images of Thomson's model, this is what they all look like. However, when Renstrøm & Bomark went and looked at Thomson's first publication on this, they found something quite different. For example, the title of Thomson (1904: 237) is:

On the structure of the atom: an investigation of the stability and periods of oscillation of a number of corpuscles arranged at equal intervals around the circumference of a circle; with application of the results to the theory of atomic structure. (emphasis added)

And in his model, the electrons are moving at high speeds. Thomson (1904: 254) says:

In this way we see that when we have a large number of corpuscles in rapid rotation, they will arrange themselves as follows: - The corpuscles form a series of rings, the corpuscles in one ring being approximately in a plane at right angles to the axis of rotation, the number of particles in the rings diminishing as the radius of the ring diminishes.

Thomson's actual model does not involve electrons evenly distributed like plums in a pudding. It involves electrons in "a series of concentric rings" (1904: 255). He does place these rings "enclosed in a sphere of uniform positive electrification" (Thomson 1904), but his actual model doesn't resemble the physics folklore version at all.

After finishing this essay, I happened to stumble upon Hon and Goldstein (2013), which confirms what Renstrøm & Bomark have said and gives more details. See also Aaserud & Kragh (2021)—an edited volume of conference papers—which contains a related article, Hon and Goldstein (2021). For more details on the history of Thomson's discovery of the electron, see Falconer (1987), and on its acceptance by the physics community, Falconer (2001).

One of the strengths of Thomson's model was that it was stable.

The problem is that the electromagnetic force is relatively strong. Two oppositely charged particles strongly attract each other. So we might expect the electron to rapidly fall down the potential well to collide with the proton. In this case, reality is somewhat counterintuitive. 

An electron and a proton can fuse into a neutron (plus a neutrino), but the reaction is endothermic, meaning that it requires a considerable input of energy. A neutron is about 0.782 MeV heavier than a proton and an electron combined. In practical terms, the electron and proton would have to have on the order of 20 million times the thermal energy they typically have at room temperature and one atmosphere. Which effectively means that it never happens. It is the sort of process we expect to find in the core of a star with very high temperatures and pressures, or indeed, in neutron stars.

By far the most common occurrence when an electron and a proton meet is that they form a hydrogen atom. This process, by contrast, is exothermic, and the excess energy generated is emitted as a photon.

This highlights the role of thermodynamics in our images of matter. Just because the electron and proton have opposite charge and experience a strong attraction, does not mean that they collapse into each other. The electromagnetic force is not the only consideration. 

To emphasise the importance of stability, Renstrøm & Bomark briefly discuss Hantora Nagaoka’s (長岡 半太郎) (1904) contemporary "Saturnian model", also published in Philosophical Magazine. The Nagaoka model was not stable and is seldom mentioned in standard works.

Thomson continued to speculate on how electrons are arranged in atoms. In 1905, Thomson gave a lecture in which says that mathematical investigation leads us to believe that electrons would form platonic solids with electrons at the vertices:

Thomson (1905: 2)

This is also misrepresented, on Wikipedia, for example, as part of Thomson's model. But Thomson does not endorse this theoretical picture and instead chooses, like a good scientist, to argue from experiment. And before long (1905:3), he is once again talking about arranging electrons in concentric rings. Wikipedia redeems a little itself by noting (without a citation) the first use of the term "plum pudding" in this connection.

The first known writer to compare Thomson's model to a plum pudding was an anonymous reporter in an article for the British pharmaceutical magazine The Chemist and Druggist in August 1906.

While the negative electricity is concentrated on the extremely small corpuscle, the positive electricity is distributed throughout a considerable volume. An atom would thus consist of minute specks, the negative corpuscles, swimming about in a sphere of positive electrification, like raisins in a parsimonious plum-pudding, units of negative electricity being attracted toward the centre, while at the same time repelling each other.

Thomson himself never used the term "plum pudding", and the model illustrated in textbooks and all over the internet is nothing like Thomson's rapidly revolving concentric rings (with his painstakingly calculated energies). Given the information he had, his model is a good attempt to balance the forces that were understood at the time.

However, things would very soon change because Thomson had a brilliant student by the name of Rutherford.

Rutherford's Model

Ernest Rutherford (1871-1937) won the Nobel Prize in Chemistry in 1908 "for his investigations into the disintegration of the elements, and the chemistry of radioactive substances." When I was growing up in New Zealand in the 60s and 70s, Rutherford was one of only a handful of internationally renowned New Zealanders (outside of sports). Rutherford was known to us as "the man who split the atom".

Renstrøm & Bomark once again outline the textbook story, illustrated with extensive quotes. The story goes that Rutherford proposed a new model of the atom that eclipsed Thomson's. Rutherford's model was like a tiny solar system with the positively charged nucleus at the centre and negatively charged electrons orbiting like tiny planets.

This is still the most recognisable picture of the atom down to the present. If you search online for images of atoms, what you mostly get is versions of tiny solar systems. The official emoji for atom is ⚛️, which is more or less the image we associate with Rutherford. Such a diagram does not appear in Rutherford's published works as far as I can see.

Once again, Renstrøm & Bomark (2022: 10) turn to the original source, Rutherford (1911), and once again find that his conclusions have been misrepresented. They say:

Rutherford did not suggest a planetary atom in 1911. He offered no suggestions of how the electrons were arranged or moved; the electrons’ exact distribution was not important for the experimental results.

The title of Rutherford (1911) is "The scattering of α and β Particles by Matter and the Structure of the Atom." Despite the latter phrase, I agree that the paper barely discusses "the structure of the atom" and constructs no models. What Rutherford showed is that the larger share of the mass of a gold atom is concentrated in a small volume at the centre of the atom.

Renstrøm & Bomark, add

The theory Rutherford presented in his paper was primarily a scattering theory, and it was not considered to be an atomic model. Rutherford’s model was met with indifference and scarcely considered to be a theory of the constitution of the atom. It was not mentioned in the proceedings of the 1911 Solvay Congress, nor was it widely discussed in physics journals.

Something that I picked up from Rutherford (1911: 688)

The deductions from the theory so far considered are independent of the sign of the central charge, and it has not so far been found possible to obtain definite evidence to determine whether it be positive or negative.

He notes that Hans Geiger and Ernest Marsden were attempting to determine this by experiment. Just three years later, Rutherford (1914: 488-489) says, referring specifically to his 1911 publication:

In order to account for this large angle scattering of α particles, I supposed that the atom consisted of a positively charged nucleus of small dimensions in which practically all the mass of the atom was concentrated. The nucleus was supposed to be surrounded by a distribution of electrons to make the atom electrically neutral and extending to distance from the nuclear comparable with the ordinary accepted radius of the atom.

Renstrøm & Bomark point out that even in the 1914 paper, Rutherford is still not suggesting that electrons are in "orbit" around the nucleus or moving in any way. His comments on the electron are the minimal corollaries of (1) a massive nucleus, (2) a positively charged nucleus, and (3) an electrically neutral atom.

In my previous essay, I showed by simple logic that these three facts are extremely important when proposing atomic structures, since there is only one configuration that can possibly balance a spherically symmetrical electrostatic field to make for an electrically neutral atom, i.e. a sphere.

Incidentally, Rutherford (1914: 488) also notes that Thomson was in fact developing a model first proposed by William Kelvin, which is also omitted from the folklore.

Lastly, Renstrøm & Bomark note another contemporary atomic structure model by John Nicholson. Nicholson managed to show that angular momentum is quantised. I'm not going to say much more about this.

Reflections

There are several takeaways here:

• Thomson (1904) did not propose a plum pudding model.
• Thomson's model involved concentric rings of negatively charged electrons rotating within a nebulous sphere of (free-floating) positive charge.
• Rutherford (1911) did not propose a model of the atom. And initially, no one thought that he did.
• Rutherford (1911) proved that the bulk of the mass of a gold atom was concentrated in the centre, but was initially unsure about the associated electric charge and did not comment on the arrangement of electrons (since they were irrelevant to his experiment).
• Later, Rutherford (1914) claimed to have said that the nucleus had a positive charge in 1911.
• Rutherford's (1914) picture is accurate as far as it goes: mass concentrated in the positively charged nucleus, surrounded by electrons which balance the electric charge to give an electrically neutral atom. But it's not a model in any formal sense. 

The papers in question are easily obtainable. I didn't even have to leave my desk. So there is no excuse for not reading them.

Renstrøm & Bomark (2022) conclude that such systemic misrepresentation is counterproductive because it can only undermine the confidence of students (if and when they discover the lie). I agree. But I take a much dimmer view of misrepresentation.

As a historian of religious texts, I am all too familiar with systematic misrepresentation. As my studies have shown, the history and philosophy of the Heart Sutra were systematically misrepresented in ways that seemed designed to elevate perceptions of its authenticity and authority. This makes me wonder about the systematic misrepresentation of classical atom models by later (quantum) physicists. As always, with a transgression, the question is "Cui bono?", i.e. "Who benefits from this?" 

As I noted in my previous essay, attempts to reify the Schrödinger equation lead to a series of incoherent, mutually exclusive metaphysics. But if we go back to the early days of quantum mechanics, there was much less in the way of pluralism. Most people accepted some form of the Copenhagen hypothesis, which required a metaphysical dualism: the world behaves in a wholly counter-intuitive manner when we don't observe it, and then, when we do observe the world, it falls into behaving intuitively. And this distinction, they say, is unavoidable. 

As I showed in my last essay, the idea that probabilities all co-exist before an observation and "collapse" at the point of observation is true of every system that we describe using probabilities. It's not that profound, unless we reify the wavefunction. 

The failure to produce a plausible metaphysics from the mathematical formalism is an ongoing problem that few physicists wish to think about, though most privately admit the problem exists. Indeed, physics folklore tells us that many physicists are openly hostile to questions about the foundations of quantum mechanics. "Shut up and calculate" and all that.

I'm not saying this is what happened, but it would not surprise me to learn that stories designed to make classical physics look trivially wrong were invented to help sell the "necessity" of embracing quantum mechanics. Along these lines, I note a comment by Hon and Goldstein (2021)

Bohr’s theory has roots in the theories of Ernest Rutherford and Joseph J. Thomson on the one hand, and that of John W. Nicholson on the other. We note that Bohr neither presented the theories of Rutherford and Thomson faithfully, nor did he refer to the theory of Nicholson in its own terms.

The metaphysical consequences of Schrödinger's approach, especially in the hands of Niels Bohr, were all too obviously problematic. Schrödinger himself was appalled by Born's "interpretation" of his wavefunction in probability terms. In a 1952 letter to Max Born, Schrödinger wrote:

"I don’t like it, and I’m sorry I ever had anything to do with it." 

(This is widely misinterpreted/misrepresented as a comment on quantum mechanics generally.)

I suspect that the quantum crowd were partly able to assert their dominance by exaggerating the failures of classical physics and using them as a stick to beat dissenters. This is an example of "there is no alternative" gas-lighting (which is very much the zeitgeist). More on this in my next essay. 

The bottom line is that there is still no coherent metaphysics associated with quantum theory. Rather, there is a growing list of incoherent metaphysics, with no overlap between any of them, and nothing like a consensus on the horizon. This confusion is reinforced by the insistence that quantum mechanics cannot be understood rationally or even imagined.

Incidentally, it is this claim of ineffability that provides leverage for mystical Buddhists to claim some kinship between their religious ideology and science. All rhetoric of "ineffability" is isomorphic. And thus, quantum mechanics becomes like a cult. And Bohr was very much like a cult leader.

But I can envisage a coherent metaphysics, the existing metaphysics of science, and I find that I can explain the foundations of quantum mechanics in a way that, while yet incomplete, is still far more intellectually satisfying than the nonsense that passes for philosophy amongst quantum physicists. In fact, there are many signs that quantum physics, with its intimate ties to the military-industrial complex, is a scam (an essay on this issue is in the pipeline).

The winners write the history. And even in the field of science, the winners are human beings who try to eclipse their antecedents and present their own view as the culmination of a telos. 

~~Φ~~

Bibliography

Aaserud, F. and Kragh, H. (eds). (2021). One hundred years of the Bohr atom: Proceedings from a conference. Scientia Danica. Series M: Mathematica et physica, vol. 1. 2015.

Falconer, I. (1987) "Corpuscles, Electrons and Cathode Rays: J J Thomson and the ‘Discovery of the Electron.” British Journal for the History of Science 20: 241-276.

Falconer, I. (2001), "Corpuscles to Electrons". In Histories of the Electron, edited by J Buchwald and A Warwick, 77-100. Cambridge, Mass: MIT Press.

Hon, G. and Goldstein B. R. (2013). "J. J. Thomson's plum-pudding atomic model: The making of a scientific myth." Annalen der physik https://doi.org/10.1002/andp.201300732

———. (2021). "Constitution and Model: Bohr’s Quantum Theory and Imagining the Atom." In One hundred years of the Bohr atom: Proceedings from a conference, 347-359. Scientia Danica. Series M: Mathematica et physica, vol. 1., 2015 (2021).

Renstrøm, Reidun and Bomark, Nils-Erik (2022). "Textbook myths about early atomic models." October 2022. DOI:10.48550/arXiv.2212.08572. [12 unnumbered pages]

———. (2024) "The Ultraviolet myth." 2024. The European Physical Society Conference on High Energy Physics. https://doi.org/10.48550/arXiv.2402.03405

Rutherford, Ernest. (1911). "The scattering of α and β Particles by Matter and the Structure of the Atom." Philosophical Magazine. Series 6. 21 (125): 669–688. doi:10.1080/14786440508637080.

Rutherford, Ernest. (1914). "The Structure of the Atom." Philosophical Magazine. Series 6, 27: 488 - 498

Thomson, J. J. (1904) "On the structure of the atom: an investigation of the stability and periods of oscillation of a number of corpuscles arranged at equal intervals around the circumference of a circle; with application of the results to the theory of atomic structure." Philosophical Magazine, Series 6, 7(39): 237 - 265. http://dx.doi.org/10.1080/14786440409463107

Thomson, J. J. (1905). “The Structure of the Atom” A Lecture Delivered at the Royal Institution. (Weekly Evening Meeting, Friday, March 10, 1905): 1-15. http://www.ub.edu/hcub/hfq/sites/default/files/Thomson_model(6).pdf

Thomson, J.J. (1906) "On the number of corpuscles in an atom." Philosophical Magazine Series 6. 11(66): 769-781, DOI: 10.1080/14786440609463496

Why Quantum Mechanics is Currently Wrong and How to Fix It.

It is now almost a century since "quantum mechanics" became established as the dominant paradigm for thinking about the structure and motion of matter on the nanoscale. And yet the one thing quantum mechanics cannot do is explain what it purports to describe. Sure, quantum mechanics can predict the probability of measurements. However, no one knows how it does this. 

Presently, no one understands the foundations of quantum mechanics. 

Feynman's quote to this effect is still accurate. It has recently been restated by David Deutsch, for example:

"So, I think that quantum theory is definitely false. I think that general relativity is definitely false." (t = 1:16:13)

"Certainly, both relativity and quantum theory are extremely good approximations in the situations where we want to apply them... So, yes, certainly, good approximations for practical purposes, but so is Newton's theory. That's also false." (t = 1:28:35)

—David Deutsch on Sean Carroll's podcast.

I listened to these striking comments again recently. This time around, I realised that my conception of quantum field theory (QFT) was entirely wrong. I have a realistic picture in my head, i.e. when I talk about "waves", something is waving. This is not what GFT says at all. The "fields" in question are entirely abstract. What is waving in quantum mechanics is the notion of the probability of a particle appearing at a certain location within the atom. Below I will show that this thinking is incoherent. 

There have been numerous attempts to reify the quantum wavefunction. And they all lead to ridiculous metaphysics. Some of the most hilarious metaphysics that quantum mechanics has produced are:

1. The universe behaves one way when we look at it, and a completely different way when we don't.
   
2. The entire universe is constantly, and instantaneously, splitting into multiple copies of itself, each located in exactly the same physical space, but with no connections between the copies.
   
3. Electrons are made of waves of probability that randomly collapse to make electrons into real particles for a moment.

None of these ideas is remotely compatible with any of the others. And far from there being a consensus, the gaps between "interpretations" are still widening. Anyone familiar with my work on the Heart Sutra will recognise this statement. It's exactly what I said about interpretations of the Heart Sutra.

Physics has lost its grip on reality. It has a schizoid ("splitting") disorder. I believe I know why.

What Went Wrong?

The standard quantum model embraces wave-particle duality as a fundamental postulate. In the 1920s, experiments seemed to confirm this. This is where the problems start.

Schiff's (1968) graduate-level textbook, Quantum Mechanics, discusses the idea that particles might be considered "wave packets":

The relation (1.2) between momentum and wavelength, which is known experimentally to be valid for both photons and particles, suggests that it might be possible to use concentrated bunches of waves to describe localized particles of matter and quanta of radiation. To fix our ideas, we shall consider a wave amplitude or wave function that depends on the space coordinates x, y, z and the time t. This quantity is assumed to have three basic properties. First, it can interfere with itself, so that it can account for the results of diffraction experiments. Second, it is large in magnitude where the particle or photon is likely to be and small elsewhere. And third, will be regarded as describing the behavior of a single particle or photon, not the statistical distribution of a number of such quanta. (Schiff 1968: 14-15. Emphasis added)

I think this statement exemplifies the schizoid nature of quantum mechanics. The Schrödinger model begins with a particle, described as a "wave packet", using the mathematics of waves. The problem is that physicists still want to use the wave equation to recover the "position" or "momentum" of the electron in the atom, as though it is a particle. I have seen people dispute that this was Schrödinger's intention, but it's certainly how Schiff saw it, and his text was widely respected in its day.

The obvious problem is that, having modelled the electron as a wave, how do we then extract from it information about particles, such as position and momentum? Mathematically, the two ideas are not compatible. Wave-talk and particle-talk cannot really co-exist. 

In fact, Schrödinger was at a loss to explain this. It was Max Born who pointed out that if you take the modulus squared value of the wave function (which outputs complex-numbered vectors), you get a probability distribution that allows you to predict measurements. As I understand it, Schrödinger did not like this at all. In an attempt to discredit this approach, he formulated his classic thought experiment of the cat in the box. A polemic that failed so badly, that the Copenhagen crowd adopted Schrödinger's cat as their mascot. I'll come back to this.

However, there is a caveat here. No one has ever measured the position of an electron in an atom, and no one ever will. It's not possible. We have probes that can map out forces around atoms, but we don't have a probe that we, say, can stick into an atom and wait for the electron to run into it. This is not how things work on this scale.

Can We Do Better? (Yes We Can!)

Electric charge is thought to be a fundamental property of matter. We visualise the electric charge of a proton as a field of electric potentials with a value at every point in space, whose amplitude drops off as the square of the distance. The electric field around a proton is observed to be symmetrical in three dimensions. In two dimensions, a proton looks something like this with radiating, evenly spaced field lines:

An electron looks the same, but the arrows point inwards (the directionality of charge is purely conventional). So if the electron were a point charge, an atom would be an electric dipole, like this:

This diagram shows that if the electron were a point mass/charge, the hydrogen atom would be subject to unbalanced forces. Such an atom would be unstable. Moreover, a moving electric dipole causes fluctuations in the magnetic field that would rapidly bleed energy away from the atom, so if it didn't collapse instantaneously, it would collapse rapidly. 

Observation shows atoms to be quite stable. So, at least in an atom, an electron cannot be a point mass/charge. And therefore, in an atom, an electron is not a point mass/charge.

Observation also shows that hydrogen atoms are electrically neutral. Given that the electric field of the proton is symmetrical in three dimensions, there is only one shape the electron could be and balance the electric charge. A sphere with the charge distributed evenly over it.

The average radius of the sphere would be the estimated value of the atomic radius. Around 53 picometers (0.053 nanometers) for hydrogen. The radius of a proton is estimated to be on the order of 1 femtometer.

Niels Bohr had a similar idea. He proposed that the electron formed a "cloud" around the nucleus. And this cloud was later identified as "a cloud of probability". Which is completely meaningless. The emperor is not wearing any clothes. As David Albert says on Sean Carroll's podcast:

“… there was just this long string of brilliant people who would spend an hour with Bohr, their entire lives would be changed. And one of the ways in which their lives were changed is that they were spouting gibberish that was completely beneath them about the foundations of quantum mechanics for the rest of their lives…” (emphasis added)

We can do better, with some simple logic. We begin by postulating, along with GFT, that the electron is some kind of wave. 

If the electron is a wave, AND the electron is a sphere, AND the atom is stable, AND the atom is electrically neutral, then the electron can only be a spherical standing wave.

Now, some people may say, "But this is exactly what Schrödinger said". Almost. There is a crucial difference. In this model, the spherical standing wave is the electron. Or, looked at from the other direction, an electron (in a hydrogen atom) is a physical sphere with an average radius of ~53 pm. There is no particle, we've logically ruled out particles.

What does observation tell us about the shape of atoms? We have some quite recent data on this. For example, as reported by Lisa Grossman (2013) for New Scientist, here are some pictures of a hydrogen atom recently created by experimenters.

The original paper was in Physical Review.

Sadly, the commentary provided by Grossman is the usual nonsense. But just look at these pictures. The atom is clearly a sphere in reality, just as I predicted using simple logic. Many crafty experiments, have reported the same result. It's not just that the probability function is spherical. Atoms are spheres. Not solid spheres, by any means, but spheres nonetheless.

We begin to part ways with the old boys. And we are instantly in almost virgin territory. To the best of my knowledge, no one has ever considered this scenario before (I've been searching the literature).

The standard line is that the last input classical physics had was Rutherford's planetary model proposed in 1911, after he successfully identified that atoms have a nucleus, which contains most of the mass of the atom. This model was debunked by Bohr in 1913. And classical physics has nothing more to say. As far as any seems to know, "classical physics says the electron is a point mass". No one has ever modelled the electron in an atom as a real wave. At least no one I can find.

This means that there are no existing mathematical models I can adapt to my purpose. I have to start with the general wave equation and customise it to fit. Here is the generalised wave equation of a spherical standing wave:

Where r is the radius of the sphere, θ and φ are angles, and t = time. Notice that it is a second-order partial differential equation, and that the rates of change in each quantity are interdependent. It can be solved, but it is not easy.

The fact is that, while this approach is not identical to existing quantum formalism, it is isomorphic (i.e. has the same form). Once we clarify the concept and what we are trying to do with it, the existing formalism ought to be able to be adapted. So we don't have to abandon quantum mechanics, we just have to alter our starting assumptions and allow that to work through what we have to date. 

An important question arises: What about the whole idea of wave-particle duality?

In my view, any particle-like behaviour is a consequence of experimental design. Sticking with electrons, we may say that every electron detector relies on atoms in the detector absorbing electrons. And there are no fractional electrons. Each electron is absorbed by one and only one atom. It is this phenomenon that causes the appearance of discrete "particle-like" behaviour. At the nano-scale, any scientific apparatus is inevitably an active part of the system.

The electron is a wave. It is not a particle. 

Given the wild success of quantum mechanics (electronics, lasers, and so on), why would anyone want to debunk it? For me, it is because it doesn't explain anything. I didn't get into science so I could predict measurements, by solving abstract maths problems. I got into it so I could understand the world. Inj physics maths is supposed to represent the world and to have a physical interpretation. I'm not ready to give up on that.

The Advantages of Modelling the Electron as a (Real) Wave.

While they are sometimes reported as special features of quantum systems, the fact is that all standing waves have some characteristic features.

In all standing waves, energy is quantised. This is because a standing wave only allows whole numbers of wavelengths. We may use the example of a guitar string that vibrates in one dimension*.

*Note that if you look at a real guitar string, you will see that it vibrates in two dimensions: perpendicular to the face of the guitar and parallel to it.

The ends of the string are anchored. So the amplitude of any wave is always zero at the ends; they cannot move at all. The lowest possible frequency is when the wavelength equals the string length.

The next lowest possible frequency is when the wavelength equals half the string length. And so on.

This generalises. All standing waves are quantised in this way. This is "the music of the spheres". 

Now, spherical standing waves, with a central attractive force exist and were described ca 1782 by Pierre-Simon Laplace. These entities are mathematically very much more complicated than a string vibrating in one dimension. Modelling this is a huge challenge. 

For the purposes of this essay, we can skip to the end and show you what the general case of harmonics of a spherical standing wave looks like when the equations are solved and plotted on a graph.

Anyone familiar with physical chemistry will find these generalised shapes familiar. These are the theoretical shapes of electron orbitals for hydrogen. And this is without any attempt to account for the particular situation of an electron in an atom (the coulomb potential, the electric field interfering with itself, etc).

So not only is the sphere representing the electron naturally quantised, but the harmonics give us electron "orbitals". And, if we drop the idea of the electron as a particle, this all comes from within a classical framework (though not Rutherford's classical framework). 

Why Does Attempting to Reify Probability Lead to Chaos?

As already noted, Schrödinger tried and failed to relate his equation back to reality. Max Born discovered that the modulus squared of the wavefunction vector at a given point could be interpreted as the probability of finding the "the electron" (qua particle) at that point. This accurately predicts the probable behaviour of an electron, though not its actual behaviour. But all this requires electrons to be both waves and point-mass particles. 

Since the real oscillations I'm describing are isomorphic with the notional oscillations predicted by Schrödinger, we can intuit that if we were to try to quantify the probability of the amplitude of the (real) spherical standing wave at a certain point around the sphere, then any probability distribution we created from this would also be isomorphic with application of the Born rule to Schrödinger's equation.

What I've just done, in case it wasn't obvious, is explain the fundamentals of quantum mechanics (in philosophical terms at least) in one sentence. The predicted probabilities take the form that they do because of a physical mechanism: a spherical standing wave. And I have not done any violence to the notion of "reality" in the process. To my knowledge, this has not been done before, although I'm certainly eager to learn if it has.

However, the isomorphism is only causal in one direction. You can never get from a probability distribution to a physical description. Let me explain why by using a simple analogy that can be generalised.

Let's take the very familiar and simple case of a system in which I toss a coin in the air and, when it lands, I note which face is up. The two possible outcomes are heads H and tails T. The probabilities are well-known:

P(H) = 0.5 and P(T) = 0.5.

And as always, the sum of the probabilities of all the outcomes is 1.0. So:

P(H) + P(T) = 1.0

No matter what values we assign to P(H) and P(T), they have to add up to 1.

In physical terms, this means that if we toss 100 coins, we expect to observe heads 50 times and tails 50 times. In practice, we will most likely not get exactly 50 of each because probabilities do not determine outcomes. Still, the more times we toss the coins, the closer our actual distribution will come to the expected value.

Now imagine that I have tossed a coin, it has landed, but I have not yet observed it (call this the one-dimensional Schrödinger's cat, if you like). The standard rhetoric is to say that the coin is in a superposition of two "states". One has to be very wary of the term "state" in this context. Quantum physicists do not use it in the normal way, and it can be very confusing. But I am going to use "state" in a completely naturalistic way. The "state" of the tossed coin refers to which face is up. And it has to be in one of two possible states: H or T.  

Now let's ask what I know and think about what I can know about the coin at this moment before I observe the state of the coin.

I know that the outcome must be H or T. And I know that the odds are 50:50 that it is either one. What else can I know? Nothing. Despite knowing to 100 decimal places what the probability is, I cannot use that information to know what state the coin is in before I observe it. If I start with probabilities, I can say nothing about the fact of the matter (using a phrase David Albert uses a lot). If I reify this concept, I might be tempted to say that there is no fact of the matter. 

Note also that it doesn't matter if P(H) and P(T) are changing. Let us say that the probabilities change over time and that the change can be precisely described by a function of the coin: Ψ(coin). Are we any better off? Clearly not.

This analogy generalises. No matter how complex my statistical model, no matter how accurately and precisely I know the probability distribution, I still cannot tell you which side up the coin is without looking. There is undoubtedly a physical fact of the matter, but as the old joke goes, you cannot get there from here.

There are an infinite number of reasons why a coin toss will have P(H) = P(T) = 0.5. We can speculate endlessly. This is why the "interpretations" of quantum mechanics are so wildly variable and the resulting metaphysics so counter-intuitive. Such speculations are not bound by the laws of nature. In fact, all such speculations propose radical new laws of nature, like splitting the entire universe in two every time a quantum event happens. 

So the whole project of trying to extract meaningful metaphysics from a probability distribution was wrong-headed from the start. It cannot work, and it does not work. A century of effort by very smart people has not produced any workable ideas. Or any consensus on how to find a workable idea. 

Superposition and the Measurement Problem

The infamous cat experiment, in all its varieties, involves a logical error. As much as Schrödinger resisted the idea, because of his assumption about wave-particle duality, his equation only tells us about the probabilities of states; it does not and cannot tell us which state happens to be the fact of the matter. The information we get from the current formalism is a probability distribution. So the superposition in question is only a superposition of probabilities; it's emphatically not a superposition of states (in my sense). A coin cannot ever be both H and T. That state is not a possible state. 

Is the superposition of probabilities in any way weird? Nope.

The fact that P(H) = 0.5 or P(H) = Ψ(coin) and that P(T) = 0.5 or P(T) = Ψ(coin) are not weird facts. Nor is the fact that P(H) + P(T) = 1. These are common or garden facts, with no mystical implications.

If we grant that the propositions P(H) = 0.5 and P(T) = 0.5 are logically true, then it must also be logically (and mathematically) true to say that P(H) + P(T) = 1. Prior to observations all probabilities coexist at the same time.

For all systems we might meet, all the probabilities for all the outcomes always coexist prior to observing the state of the system. And the probabilities for all but one outcome collapse to zero at the moment we observe the actual state. This is true for any system: coins, cats, electrons, and everything. 

Note also that this is not a collapse of anything physical. No attempt to reify this "collapse" should be made. Probability is an idea we can quantify, but it's not an entity. No existing thing collapses when we observe an event. 

Moreover, Buddhists and hippies take note, our observing an event cannot influence the outcome. Light from the event can only enter our eye after the event has occurred, i.e. only after the probabilities have collapsed. And it takes the brain an appreciable amount of time to register the incoming nerve signal, make sense of it, and present it to the first-person perspective. Observation is always retrospective. So no, observation cannot possibly play any role in determining outcomes. 

One has to remember that probability is abstract. It's an idea about how to quantify uncertainty. Probability is not inherent in nature; it comes from our side of the subject-object divide. Unlike, say, mass or charge, probability is not what a reductionist would call "fundamental". We discover probabilities through observation of long-term trends. At the risk of flogging a dead horse, you cannot start with an abstraction and extract from it a credible metaphysics. Not in the world that we live in. And after a century of trying, the best minds in physics have signally failed in this quixotic endeavour. There is not even a working theory of how to make metaphysics from probabilities. 

The superposition or collapse of probabilities is in no way weird. And this is the only superposition predicted by quantum mechanics. 

In my model, the electron is a wave, and the wave equation that describes it applies at all times. Before, during, and after observation. 

In my model, probabilities superpose when we don't know the facts of the matter, in a completely normal way. It's just that I admit the abstract nature of probability distributions. And I don't try to break reality so that I can reify an abstraction.

On the other hand, my approach is technically classical. A classical approach that ought to predict all the important observations of quantum mechanics, but which can also explain them in physical terms. As such, there is no separation between classical and quantum in my model. It's all classical. And I believe that the implications of this will turn out to be far-reaching and will allow many other inexplicable phenomena to be easily explained.

The so-called measurement problem can be seen as a product of misguided attempts to hypostatise and reify the quantum wavefunction, which only predicts probabilities. It was only ever a problem caused by a faulty conceptualisation of the problem in terms of wave-particle duality. If we drop this obviously false axiom, things will go a lot more smoothly (though the maths is still quite fiendish).

No one ever has or ever will observe a physical superposition. I'm saying that this is because no such thing exists or could exist. It's just nonsense, and we should be brave enough to stand up and say so.

There is no "measurement problem". There's measurement and there is ill-advised metaphysical speculation based on reified abstractions.

What about other quantum weirdness?

I want to keep this essay to a manageable length, so my answer to this question must wait. But I believe that Peter Jackson's (2013) free electron model as a vortex rotating on three axes is perfectly consistent with what I outlined here. And it explains spin very elegantly. If the electron is a sphere in an atom, why not allow it to always be a sphere?

Jackson also elegantly explains why the polarised filter set-up to test Bell's inequalities is not quantum weirdness, but a result of the photon interacting with, and thus being changed by, the filter. At the nano-scale and below, there are no neutral experimental apparatus.

What about interference and the double-slit experiment? Yep, I have some ideas on this as well.

Tunnelling? I confess that I have not tried to account for tunneling just yet. At face value, I think it is likely to turn out to be a case of absorption and re-emission (like Newton's cradle) rather than Star Trek-style teleporting. Again, there is no such thing as a neutral apparatus on the nano-scale or below. If your scientific apparatus is made of matter, it is an active participant in the experiment and at the nano-scale, it changes the outcomes. 

It's time to call bullshit on quantum mechanics and rescue physicists from themselves. After a century of bad metaphysics, let's put the phys back into physics!

~~Φ~~

P.S. My book on the Heart Sutra is coming along. I have a (non-committal) expression of interest from my publisher of choice. I hope to have news to share before the end of 2025.

PPS. I'd quite like to meet a maths genius with some time on their hands...

PPPS (16 Apr). I now have an answer to the question "What is waving?". An essay on this is in progress but may take a while. 

Bibliography

Grossman, Lisa. (2013). "Smile, hydrogen atom, you're on quantum camera." New Scientist. https://www.newscientist.com/article/mg21829194-900-smile-hydrogen-atom-youre-on-quantum-camera/

Jackson, Peter. (2009). "Ridiculous Simplicity". FQXi. What is Fundamental? https://forums.fqxi.org/d/495-perfect-symmetry-by-peter-a-jackson

Schiff, Leonard I. (1968). Quantum Mechanics. 3rd Ed. McGraw-Hill.